【笔记】时序电路
前言
时序电路学习笔记
http://127.0.0.1:4000/2022/06/01/555定时器/#题型1
题型1
- 判断同步时序电路还是异步时序电路,并写出时钟方程
示例:判断同步时序电路还是异步时序电路,并写出时钟方程
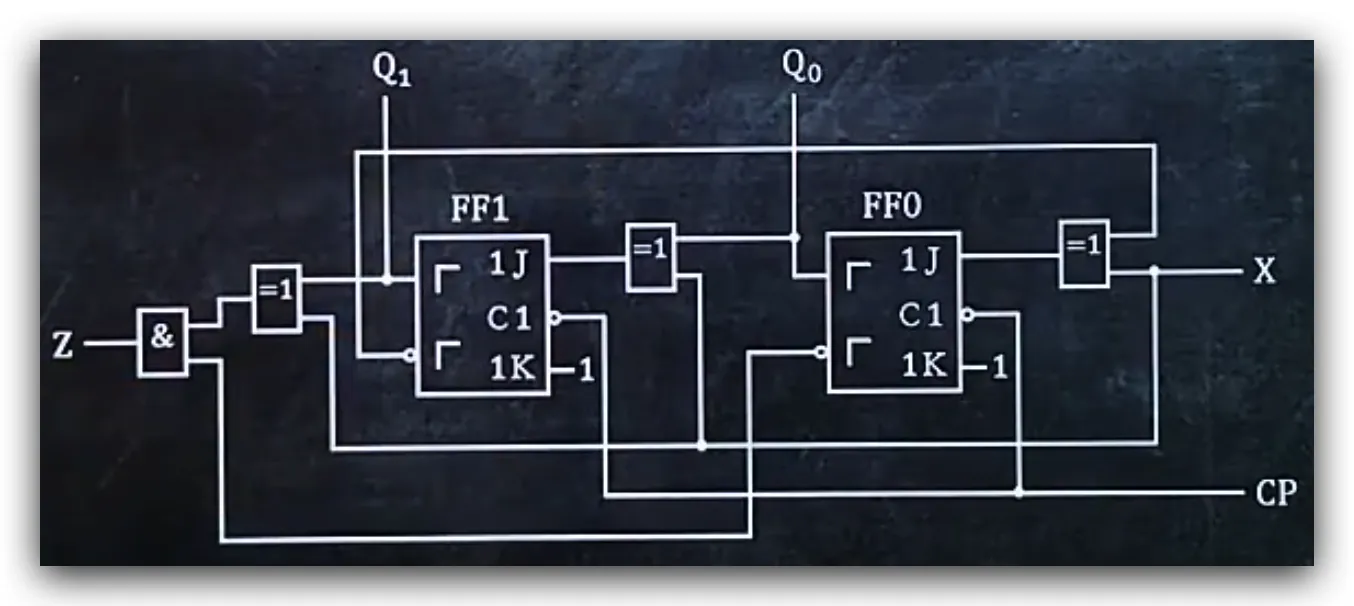
- 判断C1接口是不是连接在同一个电路上
- 如果连接在同一电路上则是同步时序电路
- 如果没有连接在同一电路上则是异步时序电路
本题是同步时序电路
- 时钟方程就是C1接口所连接电路的表达式,格式为
CP=
CP0=CP
CP1=CP
题型2
- 写出时序逻辑电路的输出方程
示例:写出时序逻辑电路的输出方程

- 输出方程就是连接Z电路的表达式,格式为
Z=,结果中如果有Q,需要将Q变为Qn
Z=(Q1n⊕X)·Q0n
题型3
- 写出时序逻辑电路的驱动方程
示例:写出时序逻辑电路的驱动方程

- 驱动方程就是连接J、K、D电路的表达式,格式为,结果中如果有Q,需要将Q变为Qn
- 如果是JK触发器,则只写出
J=、K=表达式 - 如果是D触发器,则只写出
D=表达式
J0=X⊕Q1n
K0=1
J1=Q0n⊕X
K1=1
题型4
- 写出时序逻辑电路的次态方程
示例:写出时序逻辑电路的次态方程

- 写出各个触发器的特性方程
- JK触发器:Qn+1=JQn+KQn
- D触发器:Qn+1=D
Q0n+1=J0Q0n+K0Q0n
Q1n+1=J1Q1n+K1Q1n
- 求驱动方程
J0=X⊕Q1n
K0=1
J1=Q0n⊕X
K1=1
- 将驱动方程带入特性方程
Q0n+1=(X⊕Q1n)Q0n+0·Q0n
=(X⊕Q1n)Q0n
Q1n+1=(X⊕Q0n)Q1n+0·Q1n
=(X⊕Q0n)Q1n
题型5
- 作时序逻辑电路的状态转换表
示例:作时序逻辑电路的状态转换表
Q0n+1=(X⊕Q1n)Q0n+0·Q0n
=(X⊕Q1n)Q0n
Q1n+1=(X⊕Q0n)Q1n+0·Q1n
=(X⊕Q0n)Q1n
Z=(Q1n⊕X)·Q0n
- 将输出方程和次态方程的异或化简
∵ A⊕B=A·B+A·B
∴ Q0n+1=(X·Q1n+X·Q1n)Q0n
∴ Q1n+1=(X·Q0n+X·Q0n)Q1n
∴ Z=(X·Q1n+X·Q1n)Q0n
- 分别将X=0和X=1代入式子,化简,然后绘制转换表
- 从Q1n=0,Q0n=0时开始绘制
- 当Q1n+1=0,Q0n+1=0时截止绘制
当X=0时
Q0n+1=(0·Q1n+1·Q1n)Q0n
=Q1nQ0n
Q1n+1=(0·Q0n+1·Q0n)Q1n
=Q0nQ1n
Z=(0·Q1n+1·Q1n)Q0n
=Q1nQ0n
| 现态 | 次态 | 输出 | ||
|---|---|---|---|---|
| Q1n | Q0n | Q1n+1 | Q0n+1 | Z |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
当X=1时
Q0n+1=(1·Q1n+0·Q1n)Q0n
=Q1nQ0n
Q1n+1=(1·Q0n+0·Q0n)Q1n
=Q0nQ1n
Z=(1·Q1n+0·Q1n)Q0n
=Q1nQ0n
| 现态 | 次态 | 输出 | ||
|---|---|---|---|---|
| Q1n | Q0n | Q1n+1 | Q0n+1 | Z |
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
题型6
- 作时序电路的状态图
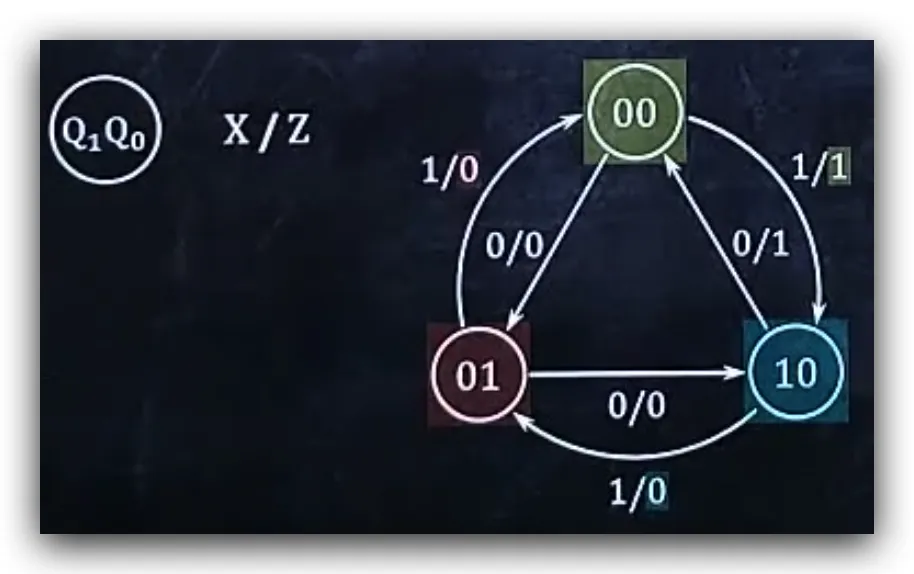
示例:作时序电路的状态图

画图
- 画出Q1Q0,并用实线圆圈圈起来,在旁边标注
位置输入量/Z - 画出所有现态的Q1nQ0n可能出现的值,并用实线圆圈圈起来
- 当X=0时,将箭头从现态的起始数值循环指向截止数值,在箭头旁标注
0/输出值 - 当X=1时,将箭头从现态的起始数值循环指向截止数值,在箭头旁标注
1/输出值
题型7
- 作时序逻辑电路的时序图
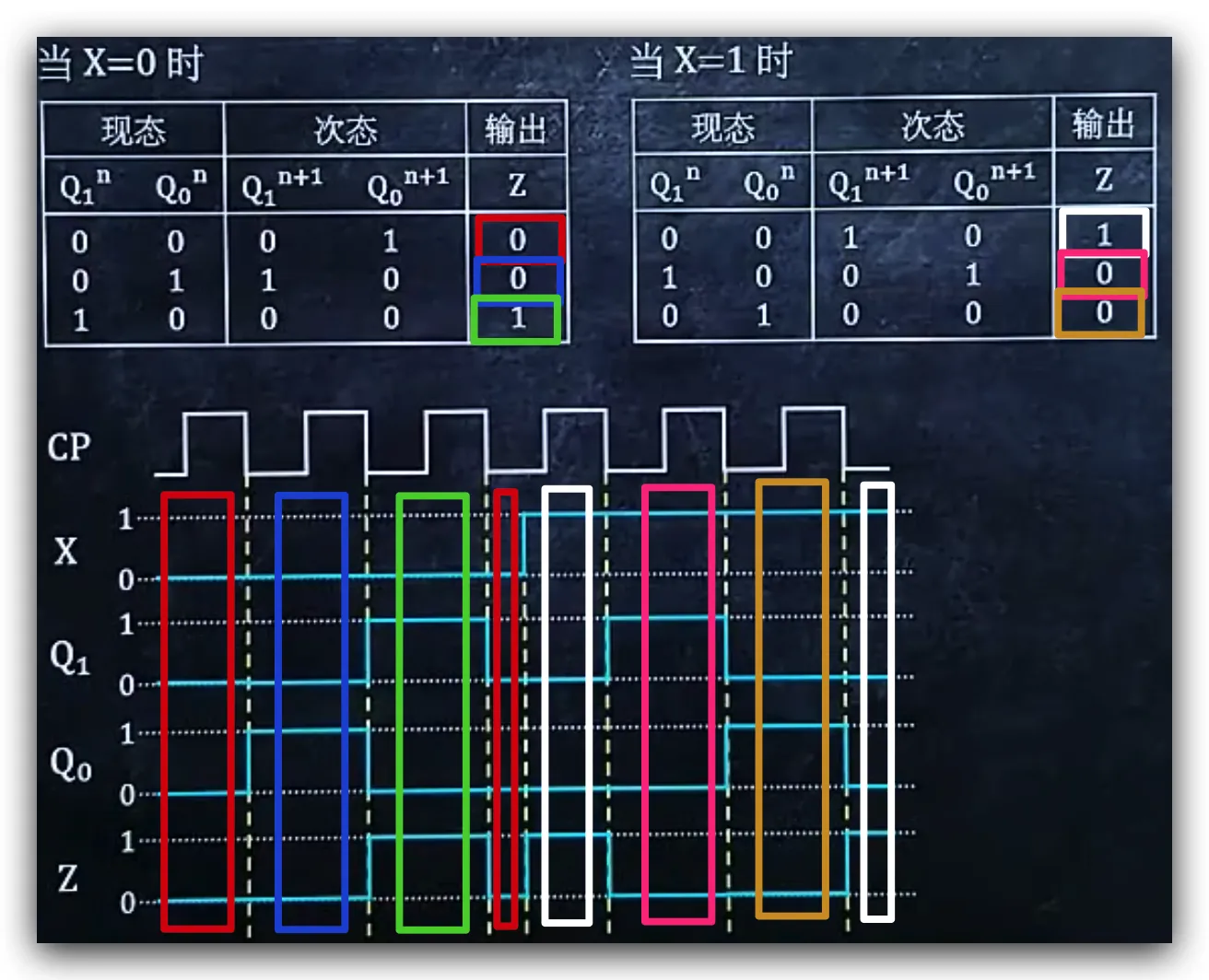
示例:作时序逻辑电路的时序图

根据状态转换表,找出行数,画CP图,突起数为状态转换表行数的2倍

- 原图观察C1接口
- 如果没有圈,则在突起左侧向下画虚线
- 如果有圈,则在突起右侧向下画虚线

- 在下方画X线,平均分为两段,前半段画0,后半段画1

- 在下方画Q1线和Q0线
- 根据当前小段的X值,查看当X等于对应值的状态表
- 根据上一段现态的Q1和Q0的值,得到次态的Q1和Q0的值,将次态的Q1和Q0的值画在Q1线和Q0线
本题中是7小段
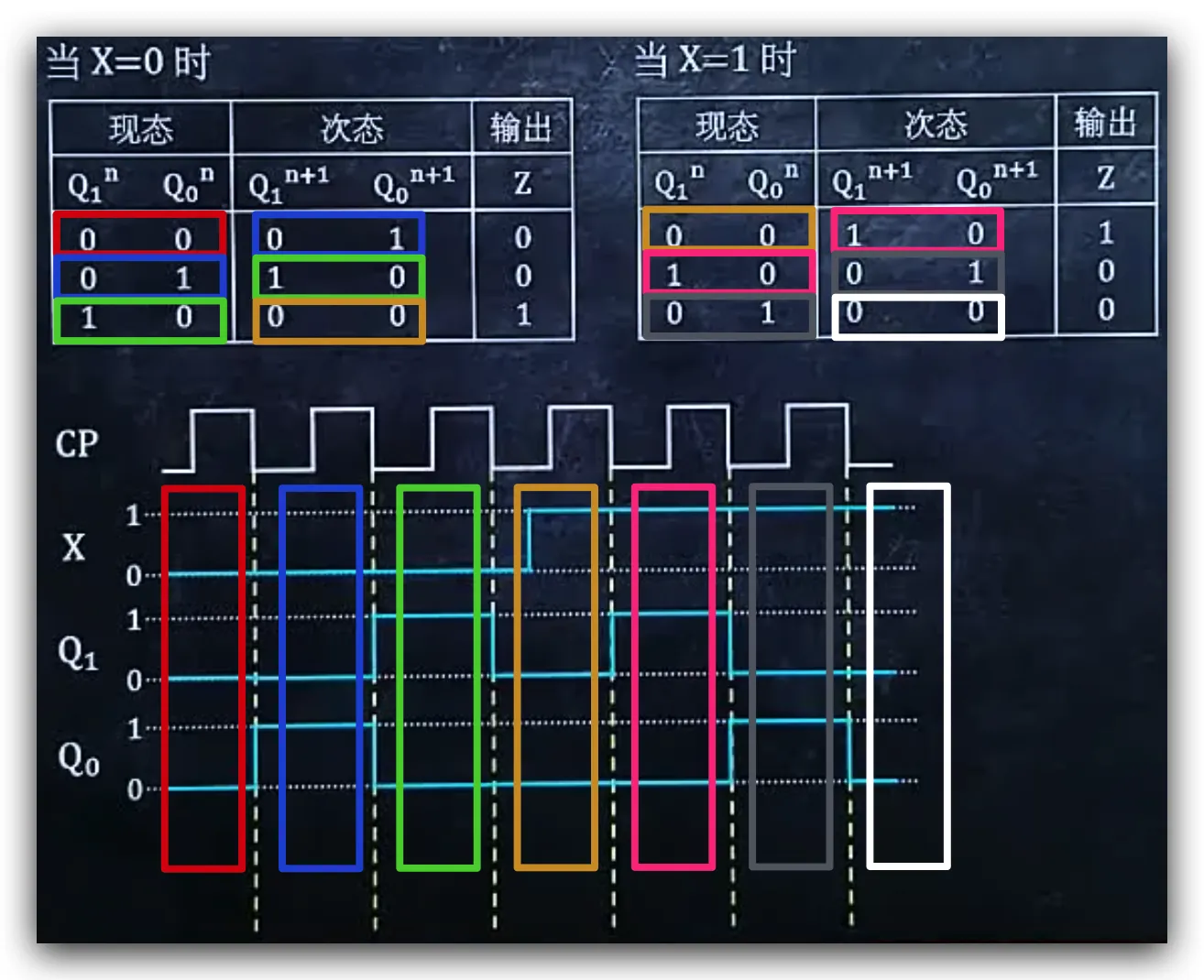
- 将X线中,不对齐的位置,向下画虚线

- 在下方画Z线
- 根据当前小段的X值、Q1值、Q0值,得到Z值
题型8
- 分析时序逻辑电路的功能
可能出现的情况:N进制加计数器、N进制减计数器
示例:分析时序逻辑电路的功能

求状态图
判断状态图中有几个圈被环形箭头指向
- 有几个圈参与环形箭头指向,就是几进制计数器
3进制计数器
- 判断状态图中的箭头方向是递增还是递减
- 如果递增,就是加计数器
- 如果递减,就是减计数器
当X=0时,3进制加计数器
当X=1时,3进制减计数器